En los conjuntos se pueden realizar algunas operaciones básicas, que parten de algunos conjuntos dados y se obtienen nuevos conjuntos. Sean dos conjuntos, A y B del conjunto universal U.
Las operaciones básicas que podemos definir entre conjuntos son;
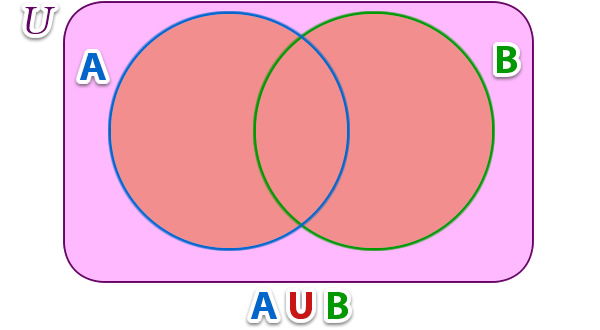
1.1- Unión de conjuntos: La unión de dos conjuntos A y B, que se escribe A U B, se define como el conjunto formado por los elementos comunes y no comunes a ambos conjuntos.
Las uniones las podemos representar en diagramas de Venn de la siguiente forma; Cuando los dos conjuntos tienen elementos en común la unión se representa de la siguiente forma;
Se llama INTERSECCIÓN de dos conjuntos A y B al conjunto formado por objetos que son elementos de A y de B, es decir: 
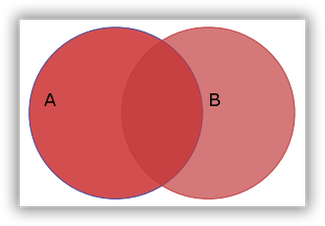
En la imagen la intersección es la parte obscura de la misma. Ejemplo: Sean A = {a, b, c, e, f}, B = {b, e, f, r, s} y C = {a, t, u, v}.
DIFERENCIA DE CONJUNTOS Dados dos conjuntos A y B, se llama DIFERENCIA al conjunto:
Luego A-B se llama complemento de B con respecto a A.
En el diagrama de Venn A-B está representado por la zona rayada.
Ejemplo: Sean A = {a, b, c} y B = {b, c, d, e}. Entonces: A – B = {a} y B – A = {d, e}. Asimismo, se llama DIFERENCIA SIMÉTRICA entre A y B al conjunto
En el diagrama de Venn la diferencia simétrica está representada por las regiones menos oscuras. (Lo que no tienen en común).
COMPLEMENTO DE UN CONJUNTO
Si un conjunto A es subconjunto de otro conjunto universal U, al conjunto A ' formado por todos los elementos de U, pero no de A, se llama complemento de A con respecto a U. Simbólicamente se expresa:
Ejemplos: a) Sean U = {m, a, r, t, e } y A = {a, e } Su complemento de A es: A' = {m, t, r} b) Sean U = {letras de la palabra aritmética} y A = { e, i, a } Determinado por extensión tenemos U = {a, r, i, t, m, e, c} A = { e, i, a } Su complemento es: A' = {r, t, m, c}
En forma gráfica:
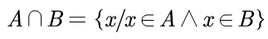
No hay comentarios.:
Publicar un comentario